Use the Graph to Describe What Transformation Has Taken Place

Gx f xh g x f x h - The graph is shifted to the left h h units. Up to 24 cash back Graph each function.

Transformations Of Graphs

3-2 Families of Graphs For each parent graph describe the transformations that have taken place in the related graph of the function.

. Use the graph to describe what transformation has taken place. Graph and determine the coordinates of the original shape as needed. That is if abisapointinthegraphoffx then ab disapointinthe graph of fxd.

Just take every point in the graph of fx and move it up a distance of d. Use the parent graph f x to graph each equation. The graph of g is a horizontal translation of the graph of f 4 units right.

A vertical translation A rigid transformation that shifts a graph up or down. When h 0 h 0 the horizontal shift is described as. 10 fx x3 5 Coo 11 - 10 -5-1-1 200 5 10 -5 10 Part 1.

If you consider fxyy-fx0 then for every substitution you perform youll witness an inverse mapping in the graph. Steps for graphing a Dilation. This occurs when a constant is added to any function.

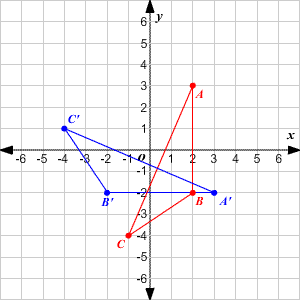
1 point А AY 4 3 12 1 B B 4. The graph of the new function is easy to describe. For example say we perform x mapsto x1 so now we have y-fx10.

H 7 h 7. The horizontal shift depends on the value of h h. Third transformation would be to shift the graph upwards by 5 units.

We can use the equation to determine the different transformations. Point form is allowed 2 marks - mark for each point b When the function is increasing and decreasing 1 mark - mark each c When the function is positive and negative 2 marks - 1 mark each d The range 1 mark If it helps you. Upon using this transformation the function will change to.

Use the graph to describe what transformation has taken place. Describe the transformations that have taken place from the graph of the first relation to the graph of the second. By this we mean that the transformation has moved point on the green graph to be at on the red graph.

Would the transformation be a rotation reflection translation or dilation. Use the graph to describe what transformation has taken place. Write an equation of a function that has a vertical asymptote at 1 and a hole at Rational Functions Day 2 1.

The mean score for all NBA games during a particular season was less than 92 points per game. List your answer below. This graph is a set G consisting of points xy where x is in the domain of the function.

There are four transformations that can occur to radical equations in the coordinate plane. Charting the Robots Dance Moves Complete the table to fill in the missing values that describe the transformation that needs to take place. Lets say you have some function yfx it has some graph.

First transformation would be to shift the graph to the right by 4 units. Changes the size andor shape of the graph. Follow the Dancing Robot Use the graph of fxx and transformations to animate the robot dancing.

Gx f xh g x f x h -. Find a a h h and k k for y x7 y x - 7. Graph the vertices of the new image and label them with prime symbols.

Write the null and alternative hypotheses. Upon using the second transformation the new function becomes. When combining transformations it is very important to consider the order of the transformations.

Giving 30 Points Just Help Me. A non-rigid transformation A set of operations that change the size andor shape of a graph in a coordinate plane. Write an equation of a function that has a slant asymptote.

The transformation being described is from f x x2 f x x 2 to gx x2 g x x 2. For example vertically shifting by 3 and then vertically stretching by 2 does not create the same graph as vertically stretching by 2 and then vertically shifting by 3 because when we shift first both the original function and the shift get stretched while only. F z 2 y 04 O horizontally compressed by a factor of 04 O vertically stretched by a factor of 04 O horizontally stretched by a factor of 04 O vertically compressed by a factor of 04 8 9 10 1.

The horizontal shift is described as. X y -- kx ky where k is the scale factor Step ï. K 0 k 0.

As an explanation for whats written above. A 1 a 1. Describe transformations that have taken place.

Combine Shifts and Stretches. Use the graphs of f and g to describe the transformation from the graph of f to the graph of g. Transformations are often easiest to analyze by focusing on how the location of specific points on the curve have changed.

Using the key points of fx -02x2 - 32x - 72 that you found in 3 describe a ALL the transformations and translations that have taken place. F z x² y 4 r - 22 O stretched vertically by a factor of 4 and translated 2 units to the right O compressed vertically by a factor of 4 and translated 2 units to the left O stretched vertically by a factor of 4 and translated 2 units up O compressed. Second transformation would be to compress the graph vertically by half.

Then list the domain and range. Use the graph to describe what transformation has taken place. Answers by tryingStep-by-step explanation.

Is a rigid transformation that shifts a graph up or down relative to the original graph. F x x2 gx x2 f x x 2 g x x 2. A 2 2 1 1 1 to 3 5 2 2 y x y x b 3 to 2 1 1 y x y x c 1 1 to 2 3 9 y y x x.

If abisapointinthegraph of fx then that means fab. Multiply the coordinates of each vertex by the scale factor. A compresses the graph if its.

List your answer below. 1 point - allnswers. The graph of g is a vertical translation 4 units up from the graph f.

List your answer below. None of the transformations introduce a bend that was not already there As such we can just track the endpoints through the transformations plot the new endpoints and. In the image above the point on the green curve corresponds to point on the red curve.

The horizontal shift depends on the value of h h. List your answer below. Because f graphs to a line segment g will also graph to a line segment.

For each parent graph describe the transformation s that have taken place in the related graph of the function.

Using Transformations To Graph Functions

Transformations Of Functions Definitions Facts And Solved Examples Cuemath

Transformations Of The 1 X Function Video Lesson Transcript Study Com